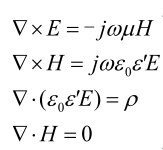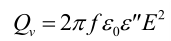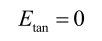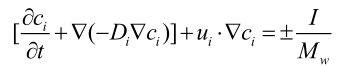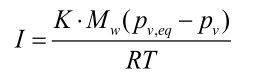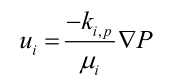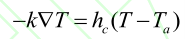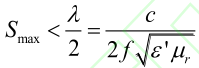三维多物理场耦合
多物理场耦合
多物理场耦合指的就是多个物理场叠加,互相影响,也是一种耦合。
现实工程中,物理场是许多的,温度场,应力场,湿度场等等均属于物理场,而我们要解决的许多问题是这些物理场的叠加问题,因为这些物理场之间是相互影响的。
如何添加多物理场:
在一个研究中,分别建立两个研究步骤,第一个研究步骤求第一个场,第二个研究步骤求第二个场。这样不需要设置求解器,但是要耦合的话需要把第一个场的变量输入到第二个场的相应位置。
微波加热数值模型
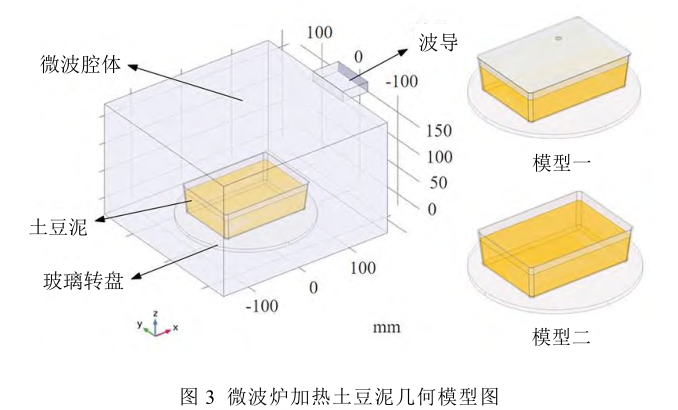
下文采用盒装土豆泥作为研究对象,基于 COMSOL模拟电磁场与传热等三维多物理场的耦合过程,构建有无包装盖膜 2 种几何模型,并将微波加热过程中电场分布和温度分布状态可视化。
微波加热餐品的过程中主要包含 4 种数学模型:模拟温度变化的传热模型、模拟水分变化的传质模型、谐振腔中场强分布的电磁数学模型和加载样品的电磁场模型。温度是反应餐品微波加热情况的重要指标,本文主要对微波加热餐品温度变化的传热模型进行研究,来预测微波加热的温度分布。
1、电磁学方程
微波加热餐品时,腔体内部为无源区域(ρ=0),求解麦克斯韦方程组得到微波腔内电磁场分布,如公式所示:
式中:E,电场强度,V/m;H,磁场强度,A/m;j,电流密度,A/m2;ω,角频率,rad/s;μ,磁导率,H/m;ε0,真空介电常数,F/m;ε',相对介电常数;ρ,电荷体密度,C/m3。
当电磁波穿过有耗介质时电磁强度减弱,损耗的电磁能作为加热源,其微波耗散能量 Qv的计算如公式所示:
式中:f,微波频率,Hz;ε″,介电损耗因子。
在微波腔中,电场的切向分量 Etan在界面处连续,金属波导和炉壁是理想电导体,适用于边界条件,如公式所示:
2、质量守恒方程
由于土豆泥餐品是土豆泥固相、水和空气的二元混合物,故可以将其看作多孔介质模型进行研究。在微波加热的过程中,土豆泥内水的浓度遵循以下质量守恒方程,如公式所示:
式中:ci (i=w,g),物质(水和气体)的摩尔浓度,mol/m3;Di,物质的扩散系数,m3/s;ui,达西速度,m/s;I,水蒸发速率,kg/(s·m3);Mw,水分子摩尔质量,kg/mol。
利用非平衡蒸发法描述水汽化相变方程,如公式所示:
式中:K,水蒸发速率常数,s-1;pv,eq,平衡水蒸汽压,Pa;pv,理想水蒸汽压,Pa;R,理想气体常数。
水气流动是由气压梯度引起的,在多孔介质模型中,流体的动量平衡遵循达西定律,如公式所示:
式中:ki,p,渗透率,m2;μi,动力黏度,Pa·s;P,水汽和空气的分压和,Pa。
3、能量守恒方程
土豆泥餐品加热时,多孔介质模型各相始终保持局部热平衡,能量守恒方程可表示为,如公式所示:
式中:Cpi,流体比热容,kJ/(kg·℃);ni,流体通量,kg/(m2·s);keff,有效热导率,W/(m·℃)。
餐品表面与空气发生热量交换,其表面的热量边界条件表示为,如公式所示:
式中:hc,对流换热系数,20W/(m2·℃);Ta,环境温度,℃。
4、几何模型与网格划分
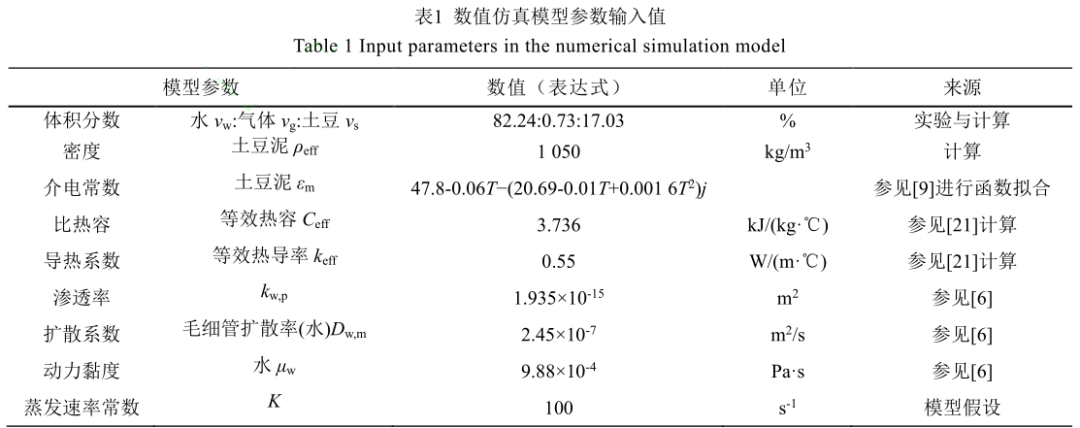
在 COMSOL 中,建立 21 L 微波炉三维模型,模型包括铜质腔体(325 mm×315 mm×202mm)、金属波导(50 mm×78 mm×18 mm)、玻璃转盘(123.5 mm×6 mm)以及包装盒(160mm×110 mm×50 mm),土豆泥厚度为 30 mm。由于土豆泥是混合物,其比热容和导热系数会随温度变化,为了减少计算量,对模型进行简化处理,利用加权公式计算进行等效替代,输入数值仿真模型的参数。
模型一为有包装盖膜餐品,认为模型含 20 mm 空气顶隙;模型二为无盖膜餐品,不含空气顶隙。网格尺寸会因求解域不同而异,为了提高精度,将模型网格划分为自由四面体单元,其中微波炉腔、玻璃转盘和土豆泥 3 个区域的网格单元尺寸分别为:2~30 mm,3~6 mm 和 2~4 mm,创建了360 635 个四面体单元,划分结果见图 4。采用 Nyquist 准则来校核最大网格单元尺寸,如公式所示:
式中:λ,波长,m;c,真空光速,3×108 m/s;ε',相对介电常数;μr,相对磁导率,1 H/m。
4、模型假设
为了方便对于加热过程的研究,对模型做出以下假设。
1)假设土豆泥和包装质地均匀,初始温度分布均匀,初始温度为 4 ℃,温度传导在加热的过程中表现为各向同性,且微波炉内空气的温度保持 25 ℃恒定;
2)假设模拟加热过程中,除了土豆泥及包装以外的所有区域均无固体传热,且包装不发生形变;
3)假设金属波导和微波炉铜壁可以看作一个理想电导体。
模拟结果
1、电场
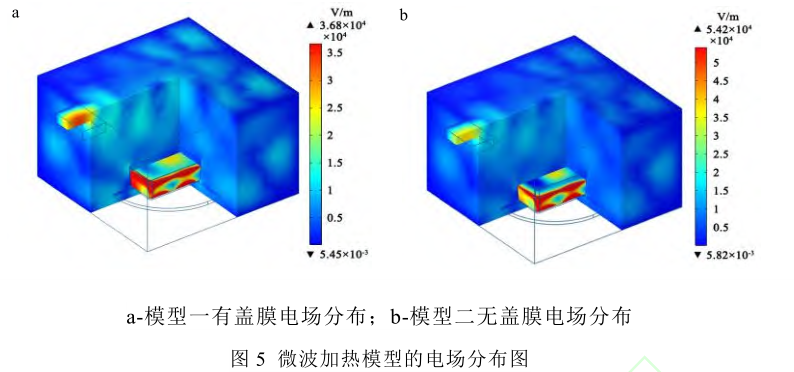
微波炉谐振腔内电场强度分布也会受土豆泥摆放位置的影响,所以应保持模型一和模型二样品放置位置的一致。微波在炉腔内传播遇到理想电导体边界发生全反射,形成驻波,微波的辐射频率为2.45 GHz,其波长为 122.4 mm,驻波为 61.2 mm,炉腔长 325 mm,除以驻波约为 5,在 X 方向上形成 5 个电场强峰。
在微波加热餐品的过程中,电磁场的分布决定了被加热物料传热场的分布,根据图 5-a 和图 5-b可以看出,2 个模型电场分布情况大致相同,电场强点和弱点的位置基本一致,区别在于场强的最大值和最小值存在明显差异,说明 PE 材质包装盖膜的存在会对谐振腔内电场强度产生削弱作用,但不会改变电场强弱点的分布。
2、温度场
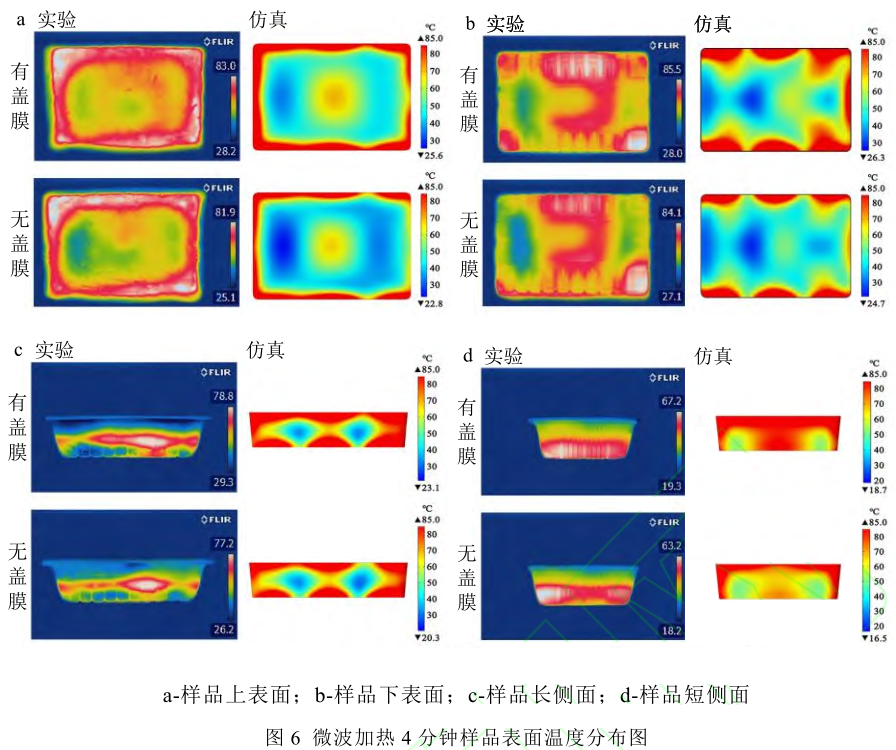
图 6-a 所示为样品上表面温度分布情况,在加热 4 min 后,样品上表面边缘产生一周高温带,最高温度有盖膜组实验值为 83.0 ℃,无盖膜组为 81.9 ℃,略低于有盖膜组,其主要原因是盖膜的存在使得加热时样品产生的湿热蒸汽难以散失,聚集在样品表面上方的空气顶隙中,从而达到了对样品表面二次加热的效果,而两组的仿真值均达到了 85 ℃。中心部位存在圆形的偏高温区,而由中心向四周过渡的区域产生了大面积的低温区,将偏高温区包围。在样品长边方向上,低温区分布在圆形偏高温区两侧。低温区包含了若干个冷点,最低温度仿真值分别达到了 25.6 ℃和 22.8 ℃,对应的实验值为 28.2 ℃和 25.1 ℃。
图 6-b 为下表面温度分布情况,同样的,在样品角隅和边缘处产生了高温区,实验最高温度达到了 85.5 ℃和 84.1 ℃,仿真最高温度均达到了 85 ℃,中心部位形成了偏高温区域,但沿长边方向从中心到两端出现了一大一小的低温区,实验最低温度为 28.0 ℃和 27.1 ℃,仿真最低温度达到了 26.3 ℃和 24.7 ℃。
图 6-c 和 6-d 为侧面温度分布情况,可以看出,在样品侧面,高温区依旧是分布在边缘处,靠近中心部位存在着低温区,但此时实验的高低温差要小于仿真的温差,这也是实际操作时热成像采集的滞后带来的影响。
PS:完整文献后台私信“文献”即可获取
 咨询服务热线:
010-56245524
咨询服务热线:
010-56245524
 百强院校名师
百强院校名师  实战落地课程
实战落地课程  持续跟踪辅导
持续跟踪辅导  大量咨询案例
大量咨询案例